LA DIFFUSION MULTIPLE DE LA LUMIERE

En diffusion multiple, l’interprétation des données expérimentales n’est possible que par l’intermédiaire d’un modèle qui spécifie la forme mathématique de l’intensité statique mesurée ou des fonctions d’autocorrélation de l’intensité diffusée. Une grandeur clé est la densité de photons en un point de l’espace qui s’obtient en résolvant l’équation de diffusion (D est le coefficient de diffusion des photons = cl^*/3, c vitesse de la lumière ) :

avec les conditions aux limites appropriées. Celles-ci dépendent de la configuration expérimentale suivant laquelle le matériau est éclairé (source ponctuelle ou étendue, détection ponctuelle ou intégrée).

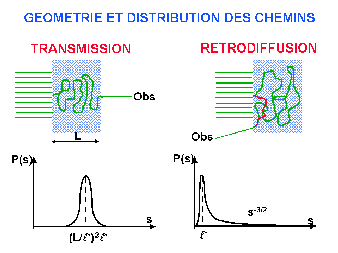
Une seconde grandeur clé qui dérive directement de la précédente est la distribution de longueur de chemin, P(s). P(s) est la probabilité qu’un photon détecté en un point ait suivi un chemin de longueur s. La forme de P(s) dépend du mode de détection En transmission, l’épaisseur du matériau traversé L fixe une distance caractéristique pour la distribution de longueur de chemin. P(s) est une distribution centrée autour de =(L/l*)2, l* qui n’est autre que la longueur moyenne d’une marche au hasard dont la distance bout à bout est L. Ainsi, pour un matériau d’épaisseur L=10mm, et une longueur de persistance l*=0.1mm, = 100m !. En rétrodiffusion, il n’existe pas de longueur caractéristique imposée par la géométie du matériau étudié de sorte que P(s) est une distribution très large incluant des chemins de toutes les longueurs.

Une fois connue la distribution de longueur des chemins, il devient possible de calculer la forme de la fonction de corrélation du champ électrique mesurée expérimentalement :

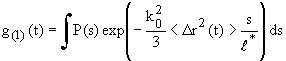
Cette expression a une interprétation remarquablement simple. Elle exprime que la décroissance de g₍₁₎(t) sur un pas du chemin est exp(-k₀²<Dr²(t)>/3) et que la décroissance sur un chemin de longueur s comprend s/l^* pas est le produit des décroissances due à chaque pas.

La connaissance de U, P(s) permet ainsi de dériver g₍₁₎(t) dans un nombre de situations pratiques. Au-delà des particularités, il est possible de dégager plusieurs tendances générales. Par simplicité, nous allons examiner le cas d’une détection en transmission. t₀ est un temps de relaxation du matériau. Comme g₍₁₎(t) décroît de exp(-t/t₀) par pas, qu’un chemin comprend en moyenne (L/l^*)² pas, g₍₁₎(t) décroît sur un temps caractéristique t = t₀(L/l^*)². Le déplacement moyen des éléments diffusants pendant ce temps est :

<Dr>_m = (l/2p)(l^*/L).

De façon remarquable, t est beaucoup plus petit que t₀ et <Dr>_m est beaucoup plus petit que l. Ainsi la diffusion multiple permet de sonder des échelles de temps et de distance très petites. Il s’agit là d’une différence majeure avec la diffusion simple qui sonde des échelles de temps de l’ordre de t₀ et des distances de l’ordre de l. En rétrodiffusion, cette caractéristique est encore amplifiée par le fait que des chemins de toutes longueurs contribuent à la fonction de corrélation. Les chemins très longs apportent une très grande sensibilité et permettent de détecter des déplacements très petits à des temps très courts. Les chemins courts sondent des échelles de temps et d’espace plus longues. La diffusion multiple en rétrodiffusion est donc particulièrement bien adaptée aux milieux comportant une distribution très large de temps de relaxation.