MICRO-RHEOLOGIE DES PATES

Nous avons utilisé la diffusion multiple pour étudier la dynamique de pâtes concentrées, notamment celles des pâtes de microgels polyélectrolytes. Les microgels sont des micro-réseaux submicroniques (diamètre ~200nm) dont le gonflement peut être contrôlé par les conditions physico-chimiques (force ionique, pH). Les particules sont déformables et, à force concentration, elles forment des pâtes dotées de propriétés rhéologiques originales. Les pâtes de microgels sont pratiquement transparentes et diffusent très peu la lumière. Pour suivre leur dynamique interne, nous les avons dopées par des sphères colloïdales de Polystyrène qui diffusent fortement la lumière et permettent de se placer dans les conditions de diffusion multiple. Le diamètre des sphères de Polystyrène est de 160nm et leur fraction volumique de l’ordre de 0.01.

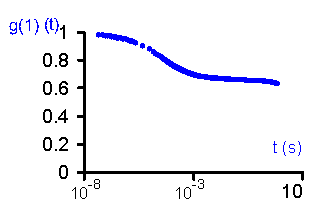
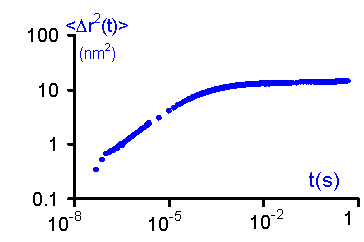
Une difficulté inhérente à ces milieux très concentrées est leur caractère non-ergodique : la fonction de corrélation en temps mesurée en un point de la figure de speckle dépend du point de mesure à cause de la présence de fluctuations " gelées ". Nous avons utilisé et mis en oeuvre divers protocoles pour remonter aux fonctions de corrélation d’ensemble. Une fonction de corrélation d’ensemble présente l’allure caractéristique de celle qui serait mesurée dans un système vitreux : g₍₁₎(t) décroît vers un plateau qui persiste jusqu’aux temps les plus longs accessibles. La décroissance de g₍₁₎(t) à temps court est analogue à une relaxation de type b. L’absence de relaxation de type a à temps long exprime la présence de configurations locales piégées pendant des temps très longs. Il est intéressant de noter l’étendue du domaine de temps exploré ! Les fonctions de corrélation donnent accès au déplacement quadratique des sondes dans la pâte au cours du temps . Ces courbes sont bien décrites par des fonctions exponentielles étirées qui traduisent la présence d’une distribution très large de configurations (en rouge).Cette modélisation donne accès aux propriétés rhéologiques des pâtes : G’, G’’, t_b. Ces grandeurs, et en particulier le temps t_b, suivent des lois d’échelle remarquables qui permettent de décrire les propriétés des pâtes de façon universelle, indépendamment des nombreux détails physicochimiques, et qui éclairent les mécanismes locaux qui régissent les propriétés dynamiques des pâtes.